Do higher interest rates raise the exchange rate?

This post follows my previous post, on whether and how higher interest rates lower inflation. The same issues arise in the most basic question of international monetary economics: Do higher interest rates raise the value of the dollar, and if so how? What is the simplest, most basic, set of necessary ingredients required to justify this time-honored belief?

In the end, this issue seems just as unsettled and for the same reasons. Modern economics wants to produce the wrong sign and fixing that invoves some equilibrium selection skulduggery. Asking the question integrating monetary and fiscal policy resolves many of those issues but has not yet produced a simple textbook model with the desired sign.

As with inflation, there is a Standard Doctrine, with standard intuition. Higher interest rates make dollar investments more attractive. People want to buy dollars to make those investments. They drive up the value of the dollar. This intuition is full of fallacies. First, high nominal interest rates are not necessarily high real interest rates. Already this story jumps the gun to some sort of price stickiness. Second, you don’t need to hold dollars very long to make US investments. To buy a US stock, say, you need to hold dollars for a day or two at most. So a desire to hold higher yielding US assets does not obviously raise demand for a scarce quantity of dollars. Third, central banks don’t control money supply anyway, they control interest rates and allow money supply to expand. And more.

How does simple modern intertemporal economics think about the question? As with inflation, we start with the flexible-price neutral benchmark. In that benchmark the exchange rate is just the ratio of price levels. (I start also with a single good.) So take your theory of the price level, divide the domestic by the foreign price level, and you get the exchange rate. If you start with MV=PY, higher money growth raises the domestic price level and thus lowers the exchange rate. It takes more dollars to buy a foreign currency. If you start with nominal government debt / price level = expected present value of surpluses, a fiscal shock that raises the price level lowers the exchange rate. Obviously, the latter is the kind of theory I want to construct. But as with inflation, we want to understand also how interest rate targets affect inflation.

With an interest rate target and flexible prices, we start again with the Fisher relation, interest rate = real rate + expected inflation, and the real rate is not affected by monetary policy,

\(i_t = r + E_t \pi_{t+1}.\)

As last time, in the flexible-price world, and thus in the long-run of a sticky price world, higher interest rates raise expected inflation. Thus, they lower the exchange rate, the opposite of the sign we’re looking for.

Here I implicitly kept the foreign currency’s value fixed. To talk about exchange rates explicitly, we subtract this Fisher relation across countries. Or we express and intuit the answer directly: A higher interest rate at home than abroad must be matched by expected depreciation of the home currency. Using * to denote the foreign country,

\(i_t - i^\ast_t =- E_t(e_{t+1}-e_t).\)

Here e_t is the exchange rate in foreign currency per dollar, so that a larger value means a more valuable dollar. If the interest rate is higher in the US than in the EU, then people will try to invest in the US rather than EU. But the rate of return for a European, investing in the US, is equal to the US interest rate less depreciation of the dollar. The cost for a US investor who wants to borrow cheap euros to invest in the US is the european interest rate plus depreciation of the dollar. Thus, this process stops, and the economy is in equilibrium, when people expect the dollar to depreciate just enough that the real rate of return is the same for both Euro and dollar investments.¹

(This prediction doesn’t hold particularly well in reality, but that’s not the point here. We are trying to find the simplest model that generates the right sign, we add frictions later. If we need frictions to get the sign right, well that’s news too and tells us the effect may be more ephemeral than we think.)

As with inflation, though, we can have the current exchange rate e_t jump down the instant the interest rate i_t jumps up. Then, the dollar can start depreciating. The same equation at time t-1 only pinned down the expected value of the exchange rate e_t . (If this all sounds familiar after the last post, it should. This whole discussion is also a great example of why it is vital to write down economic models with equations. Would the distinction between expected and unexpected exchange rate and t vs t+1 changes have been at all coherent without the equation?)

That higher interest rates make the exchange rate jump up and then start depreciating is already the standard view in academic international economics. One of the major hurdles for inflation —getting higher interest rates to produce a future disinflation — is easy here.

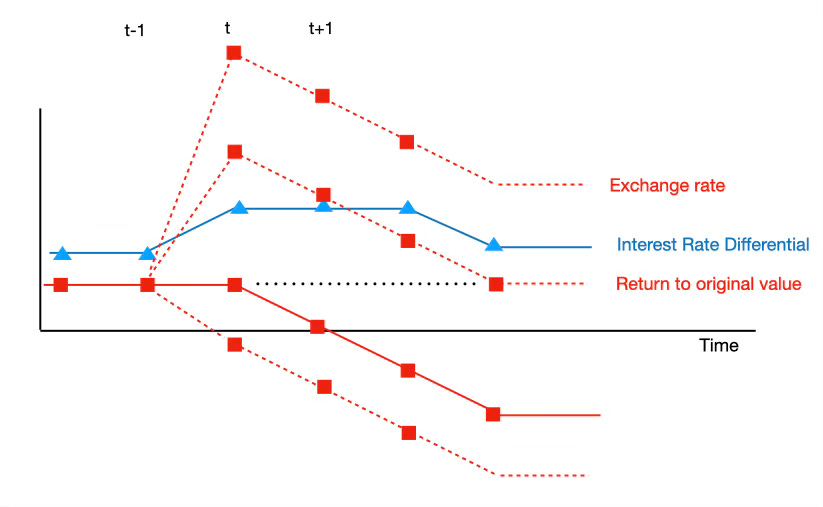
The picture shows the possibilities. Suppose the interest rate rises for three periods, as shown. What happens to the exchange rate? Well, a higher interest rate at t must imply expected depreciation from t to t+1, so there must be three periods of depreciation while the interest differential persists. The solid red line shows that possibility. Once the interest rate returns to normal, the exchange rate stops moving, but at a permanently lower level. (The exchange rate is a difference of price levels, so it keeps going down as long as inflation is higher.)

But as before, the international Fisher equation is by itself not a complete model. It does not say what happens to the exchange rate at time t. That rate can jump up or down. The dashed lines show three possibilities. The exchange rate could jump down and then continue on its depreciation. The exchange rate could jump way up, and then depreciate. Or, the exchange rate could jump up just enough so that expected depreciation brings it back to its original level.

We’re back in the equilibrium-selection swamp of my last post. Standard models now add ingredients in order to pick the equilibrium where the exchage rate goes back to its earlier level. So, the standard answer: Why do higher interest rates raise the exchange rate? Well, higher interest rates cause a depreciation. But the exchange rate first jumps up so that it can now depreciate back to its initial level.

But why should the exchange rate revert to its earlier level? That is the Achilles heel of this story. There is no natural force that brings nominal exchange rates back. Since the exchange rate is a ratio of price levels, we need to think about what the price-level nominal anchor is.

If you are a monetarist, the only way to raise the interest rate in the first place was to increase the rate of money growth. (Yes, increase. We’re still in flexible-price land). That raises inflation, and raises the nominal interest rate. At the end of the epsisode, the US has a larger money stock outstanding than the EU, so of course will have a higher price level and a permanently lower exchange rate. At the beginning of the episode, time t, the higher money growth has not raised the money stock, so there is no immediate change in the exchange rate. The monetarist picks the solid line.

New-Keynesians fill in the equilibrium selection, as usual, with central bank threats to explode the economy for any other value. An interest rate with a Taylor principle keyed on the exchange rate or price level can do the trick. If the price level or exchange rate does not go back to its original value, the Fed will induce a hyperinflation or deflation. Abhoring such explosions, the economy settles on the chosen equilibrium. Mike Woodford’s Interest and Prices describes such “Wicksellian” policies. A variety of similar other off-equilibrium threats are also used. This is, as far as I can tell, the standard approach of currrent international macro. Several international colleagues I asked to explain why models predict a return to the original exchange rate described various snake pits of off-equilibrium equilibrium-selection threats.

As before, the major problem with this suggestion is that our Fed does no such thing. It does not destabilize the economy or make other threats to select equilibria. Moreover, it pays no attention to the price level and precious little to the exchange rate. A feedback rule from inflation to interest rates is at least superficially plausible. Price level or exchange rate equilibrium-selection rules for our Fed are not. At best, equilibrium-selection threats are ways the Fed could choose one of multiple equilibria, policy proposals, but not descriptions of how the Fed does choose multiple equilibria.

Fiscal theory, of course, offers a simple way to complete the model and pick one equilibrium. If the price level jumps down, and the exchange rate jumps up at time t, then government bonds become worth more. Equivalently, the government will take in less tax revenue at the same tax rate (nominal tax revenue = tax rate x price level x real income). The government has to raise real tax revenue or cut real spending to pay back bondholders. If the government does not change fiscal policy, then the price level and exchange rate at time t does not move.

To the answer “what happens to the exchange rate at time t?” the fiscal theorist responds that depends on fiscal policy. If a fiscal tightening accompanies the interest rate rise, the exchange rate rises. If there is no change in fiscal surpluses, then the exchange rate does not move, and we follow the solid line. With that sensible definition of what monetary policy can achieve by itself, we follow the solid line.

(To generate the higher interest rate and expected depreciation in fiscal theory, the government sells more bonds without changing surpluses. Then at time t+3, nominal debt has increased, so with no change in surpluses, the price level increases as well. This is just like the monetarist answer, with debt in place of money.)

The fiscal theorist would add that the same fiscal shock can produce the exchange rate rise without the subsequent depreciation. And the fiscal theoriest might point out that the new-Keynesian could do the same thing with equilibrium selection policy. The exchange rate rise has nothing essential to do with higher interest rates.

The fiscal theorist can also produce the conventional response, and I think this is a promising direction to write such. models. The government wants to raise the exchange rate temporarily. It does so with a fiscal tightening. But the government wants to slowly restore the previous exchange rate. It does so with the higher interest rates, additional bond sales with no surpluses, and gentle expected depreciation. More generally, fisal and monetary policy may well want to stabilize the price level or long-run exchange rate, and they can do it without lots of equilibrium-selection games. Such a simple commitment gives a reason for the return to the original exchange rate — except when governments want to abandon that commitment, devalue, and allow a permanent change.

As an additional way to see the problem with the standard story, notice that I only plotted the response to a temporary interest rate rise. What if the interest rate rise is permanent? That shouldn’t cause a problem for economic theory. A country can choose a permanently higher inflation than other countries, and should see its exchange rate permenently continue to depreciate. We see lots of permanent and persistent depreciations with inflation around the world. But you can’t close the model with an assumption that the exchange rate returns to its original level in that case.

Add frictions, you say. Sticky prices, multiple goods, transport costs, financial frictions, and more. And rightly. But just as with my last post, stop first and think. I have expressed the essentials of the standard view without any frictions. It does not need frictions. So frictions will just draw out these dynamics without changing the basic economic story. And as far as I can tell, that’s just what they do.

Still, I think integrating exchange rates and inflation responses to monetary policy is a promising way to unravel these puzzles, and I write this post in part as my thinking aloud in advance of that project. The exchange rate and measured inflation give us two measures of the effects of monetary policy. The exchange rate is a lot less sticky, so should give some sense of where prices are going in the long run. Identification is always a problem in empirical work. However, most US Fed decisions are made in response to inflation and unemployment news, so perhaps plausibly exogenous for measuring exchange rate effects. For other countries, the opposite may hold.

Of course, the exhange rate empirical literature is full of puzzles. The relation above between interest rates and expected depreciation does not hold well in the data. Persistent inflation differentials should match persistent depreciation, but that seems to take a very long time. Yes, the Yen is about 1/100 the value of the dollar, and prices in Japan all have two more zeros on them, but it’s hard to see that long run in time-series estimates. And the relation between interest rates and domestic inflation has just such puzzles.

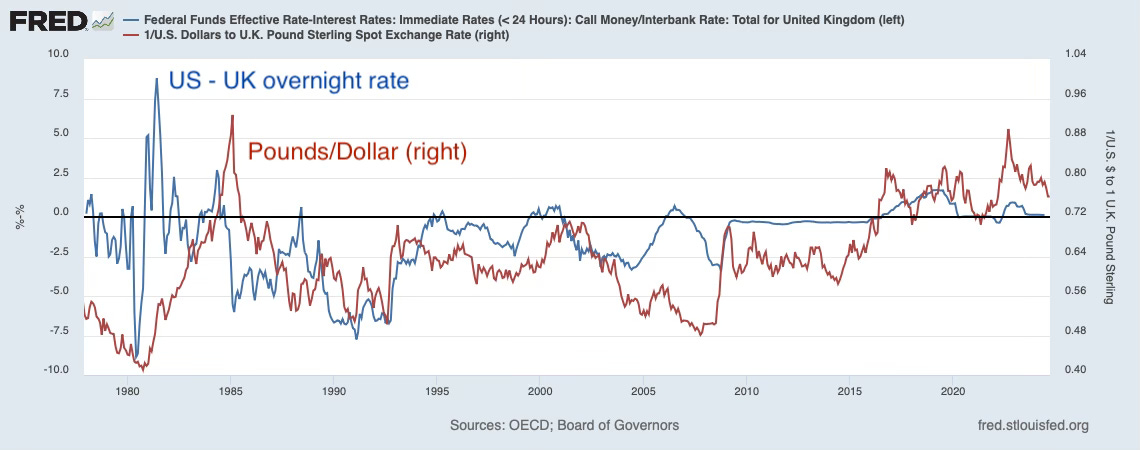
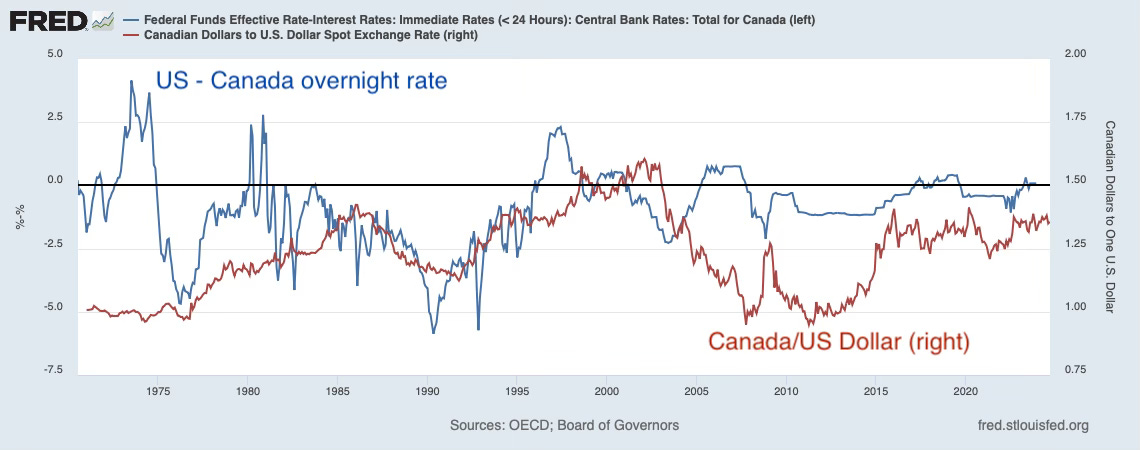
I started this post with the premise that the evidence for the Standard View that higher interest rates raise the exhange rate is a lot stronger for the evidence that higher interest rates lower domestic inflation. The view goes back forever. The Bank of England under the gold standard routinely raised interest rates to defend the Pound. I thought I’d just show the obvious fact with a few graphs. Here are the graphs:

In each ase the blue line is the US Federal Funds rate minus an overnight rate in the selected country. The red line is the exhange rate, measured as foreign currency/US dollar, so that up represents appreciation of the dollar. I was hoping for a positive correlation, or at least episodes in which a sharply higher interest rate in the US correlates with a stronger dollar. If you squint, I guess you can see a correlation and some episodes. But I’m chastened by the fact that I had one of the exchange rate graphs upside down when I wrote the first draft of this post, and that looked just as good.

This failure is hardly definitive. Lots of other forces move exchange rates around. One of the major changes in monetary policy analysis in the last decades is that, from Milton Friedman’s view that the majority of business cycles and inflation or deflation episodes come from monetary policy, we now find that monetary policy shocks count for tiny fractions of the variation of output and inflation. Other shocks (financial crisis, pandemic) and monetary policy rules matter more. Similarly, contemporary international economics assigns a tiny fraction of the variance of exchange rates to monetary policy actions. The contemporary view is distresslingly weighted to exogenous sentiment, liquidity and noise trader buyuing and selling pressure against fairly static and sloped demand curves in my view, but the important point is that even if higher interest rates can raise exchange rates, we do not expect that correlation to jump out at us because so much else is going on.

Still, it would have been nice to show some clear evidence for this longstanding view, rather than send us off to the same equivocal VAR analysis that underlies interest rates and inflation. If you know of better graphs, let me know.

The bottom line: The standard view of how interest rates affect exchange rates suffers many of the same problems as the standard view of how interest rates affect inflation. For young researchers, this is great news. The most basic policy exercise of all in international economics is up for grabs. I am hopeful that fiscal theory at last solves the gaping multiple-equilibrium hole, and that by treating inflation and exchange rates together as joint outcomes of policy we will make some big progress. That will need some frictions, and the big quesiton is just what are the minimal set of frictions needed to get a simple model going.

As I am not in as close touch with the international literature as I am with domestic macro, this post is a bit more tentative. I welcome comments, especially if I have missed some important points and succcessful resolutions of these puzzles.

1. To connect the Fisher equation and the interest rate parity condition, the exchange rate is

\(e_t = p^\ast_t - p_t\)

and inflation is

\(\pi_t = p_t - p_{t-1}.\)

Then you can see the two equations are equivalent.