Fiscal Theory Parables

We often understand economic theories and connect them with the world through simple parables and conceptual experiments. Today, I’m going to pass on a few such parables. These are all recycled from deep in the Fiscal Theory of the Price Level. But in reading many fiscal theory and related papers and commentary, I realize that only the first parable is commonly understood. The other parables are just as useful, and bring to life less well understood aspects of fisacal theory.

The Surplus Shock

This is the parable most people know. The price level adjusts so that the real value of government debt equals the present value of primary surpluses, just as a stock price adjusts so that the value of the stock equals the present value of its dividends. So, a deficit that does not come with credible promises of subsequent surpluses, or a decline in expected surpluses — an age of intractable deficits — results in inflation.

This is a good parable, but it is not the only parable. Later parables overturn much of the impression you get from this one of what the fiscal theory is all about.

Equations:

The valuation equation:

\(\frac{B_{t-1}}{P_t} = E_t \sum_{j=0}^\infty \beta^j s_{t+j} \;\; (1)\)

where B = nominal debt, P = price level, E = expectation, 𝛽 = a constant discount rate and s = real primary government surpluses (tax-spending). (I have complained to Substack about the appearance of Latex equations in email. The web version looks much better, at grumpy-economist.com.)

If the surpluses decline, since debt B_t-1 is predetermined, the price level P_t must rise. More explicitly, unexpected inflation comes from an unexpected decline in the present value of surpluses:

\(\frac{B_{t-1}}{P_{t-1}} (E_t - E_{t-1}) \left( \frac{P_{t-1}}{P_t} \right) =( E_t-E_{t-1}) \sum_{j=0}^\infty \beta^j s_{t+j} \; \; (2)\)

The Twin Parables of Debt

But where does the debt B come from? The government’s levers here are both nominal debt B and surpluses s. There are two possibilities:

1) If the government sells debt and raises future surpluses at the same time, the debt sale has no effect on bond prices, interest rates, or inflation. It raises revenue that the government can use to fund a deficit. The future surpluses then slowly pay off that debt.

2) If the government sells debt without raising future surpluses, then the government creates future inflation, lowers the bond price, raises the interest rate, and raises no revenue.

The former is like an equity offering. The company issues shares, and promises higher future dividends. The price per share is unaffected, and the firm raises revenue that it uses to make investments that in turn create the future dividends. The latter is like a share split: the firm doubles the number of shares without raising expected dividends. That halves the stock price, but raises no revenue.

The former is normal debt policy, with which we are familiar. We expect that issuing debt raises revenue and funds deficits. That only happens, however, to the extent that people believe the debt will be followed by surpluses to pay off the debt. But the latter is possible too.

This post was prompted in part, by a very good fiscal theory paper, which incidentally stated that debt B_t-1 is the result of financing past deficits. No! Debt B_t-1 can come from operations that involve no deficits whatsoever! Don’t forget the second parable.

Equations:

Look at the end of period t-1, when the government sells debt B_t-1. (The previous equation holds at the beginning of period t.)

\(\frac{Q_{t-1} B_{t-1}}{P_{t-1}} = \frac{1}{1+i_{t-1}} \frac{B_{t-1}}{P_{t-1}} = E_{t-1} \sum_{j=0}^\infty \beta^{j+1} s_{t+j} \; \; (3)\)

Here, Q_t-1 is the bond price at time t-1, B_t-1 is debt sold at time t-1, and i_t-1 is the nominal interest rate at time t-1. The numerator is now the market value of debt.

The beginning of period t-1 valuation equation reads as before, just with t-1 in place of t.

\(\frac{B_{t-2}}{P_{t-1}} = s_{t-1} + \frac{Q_{t-1}B_{t-1}}{P_{t-1}} = s_{t-1} + E_{t-1} \sum_{j=0}^\infty \beta^{j+1} s_{t+j}\; \; (4)\)

In words, money printed up to redeem debt at the beginning of t-1 is soaked up by surpluses at t-1 plus debt sales at t-1. The real value of debt sales at t-1 equals the present value of surpluses from t forward. This equation determines the price level P_t-1, as per the first parable.

Now we can ask, what if the government sells more debt B_t-1 at the end of t-1? The price level P_t-1 is already set. So, if the government sells more B_t-1 with no change in surpluses s_t-1, s_t, s_t+1 …, so the only thing that can change is the bond price Q_{t-1 .} That price must decrease, the interest rate must increase, and by

\(\begin{align} Q_{t-1} = \frac{1}{1+i_{t-1}} &= \beta E_{t-1}\left(\frac{P_{t-1}}{P_t}\right) \; \; (5)\\ i_{t-1} & \approx r + E_{t-1}\pi_t \end{align}\)

the future price level and inflation increase. The same “dividends” are split between a larger number of “shares” B.

If the government sells more debt B_t-1 and simultaneously increases surpluses s_t, s_t+1 etc. by just the right amount, then the bond price Q_t-1, interest rate i_t-1 and all price levels in (3) can remain unchanged. In (4) the extra debt can finance a deficit, a lower or negative value of s_t-1.

Expectations and Institutions

We are used to debt sales that raise revenue, finance deficits, and hence investors must expect future surpluses. Selling more debt without having any effect on fiscal surpluses — the “share split” operation — seems a bit weird.

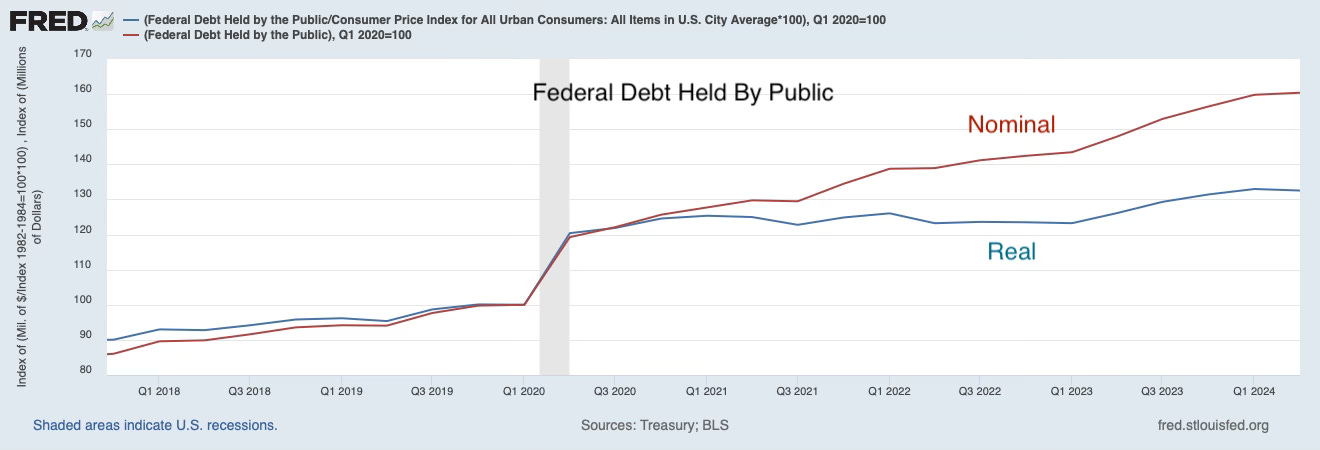
In broad brush, we have just lived through such an operation.

The nominal value of debt increased 60% since 2020:1. The real value of debt has only increased 30%. Inflation made up the difference, of course. Viewed through the lens of this simple flexible price model, the initial 20% covid surge in debt was financed by raising expected surpluses, which raise the value of debt. The subsequent debt is almost all debt that does not correspond to surpluses and only raises inflation. Of course that story does not account well for the dynamics, and real interest rate variation. You need sticky prices and long term debt for the dynamics. But an increase in debt with no increase in future surpluses, that just causes inflation is not such a weird thing. We just saw something like it!

In more normal times, the central bank buys and sells government debt in exchange for money, but has no power or authority to change taxes or spending. Selling more or less debt without changing surpluses is a stylized version of an open market operation.

How do people know whether to expect more dividends or not when a company announces a doubling in the number of shares? How do we distinguish a 2-1 split from a share issue? If we just look at expected dividends, it all seems a mystery of expectations management. But of course the two operations are conducted in very different institutional contexts, with even different legal requirements. It is very clear to investors whether the operation is a 2-1 split or a share issue that wants to raise revenue.

How do people know whether a sale of additional debt comes with extra future surpluses, is designed to raise revenue and finance a deficit today, or if it comes with no extra future surpluses and is designed just to raise interest rates? If we think just about expected surpluses, it seems a mystery of expectations management. But of course the two operations are conducted in very different institutional contexts. One is conducted by Treasury auctions, the other by Federal Reserve purchases. It is clear whether the operation is designed to raise revenue or to manipulate interest rates.

There is a deeper point here. Where do expected surpluses come from? No, we do not envision Joe and Jane sitting around the kitchen table poring over CBO deficit projections for 2045. Expectations are conveyed by institutional structures.

The interest rate target

Rather than sell a fixed quantity of debt B_t-1 with no change in surplus, and watch interest rates adjust via (3), the government can instead announce a nominal interest rate i_t-1, and announce it will sell as many nominal bonds as people want at that rate, with no change in surpluses. Now (3) describes how many bonds B_t-1 the government will end up selling at the interest rate target.

This parable describes how the government can set a nominal interest rate target, even in the frictionless fiscal theory of the price level. Many models posit an interest rate target without being particularly clear just what the government does to enforce that target. To nail a price, you have to offer a flat supply curve of something!

Once the Fed sets the interest rate target, that sets expected inflation by (5), and now we know how — by setting the amount of debt B that shows up on the left side of the FTPL. Central banks matter in FTPL!

The surplus shock is actually quite limited as a parable. Fiscal policy only sets unexpected inflation, for one period, in this simple model. Monetary policy has full control over expected future inflation. The B matters a lot!

The steady price level with varying debt and deficits

A standard picture of fiscal theory involves lots of debt and deficits that correspond to lots of volatile inflation. (See for example just how inane Chat GPT’s summary of FTPL is, here at Marginal Revolution. This parable will directly correct the AI.) FTPL is, as some have told me, a theory for turbulent times in Latin America, for currency crashes, for “nearly insolvent” governments (Chat GPT again) not for (once upon a time) low inflation countries like the US. That’s not true. The fiscal theory of inflation can also be the fiscal theory of no inflation.

Think of a country that regularly borrows, runs deficits, and runs up debt in bad times, but then slowly pays off its debt in the following good times. Deficits are always matched by opposite changes in subsequent surpluses. There is then no variation at all in the present value of surpluses. And there is no inflation at all, and a completely steady price level.

Moreover, times of high debt — lots of past deficits — will be times with high subsequent surpluses. Debt will forecast surpluses. A regression of surpluses on debt will show a positive coefficient. This economy will show all the standard signs of “passive” fiscal policy — surpluses respond to debt — used to test for “passive fiscal” regimes, yet fiscal policy is decidedly “active.” The surpluses may even be completely exogenous.

FTPL can apply to perfectly normal times, “good” fiscal policy, with a steady price level, debts that rise and fall and are always repaid.

Equations:

Fiscal Theory of the Price Level has some elegant examples. Here is a simple example, though less elegant (also in FTPL however. Suppose the surplus follows a simple MA(1),

\(s_t = \varepsilon_t - (1+r)\varepsilon_{t-1}\)

with 𝛽 = 1/(1+r). (Yes, the lagged term is bigger than one. There is nothing wrong with that for this purpose. This is deviation around a constant s, so that debt and price level are positive.) Innovations to the the present value of the surplus then give

\(\begin{align} (E_t -E_{t-1}) \sum_{j=0}^\infty \beta^j s_{t+j} &= (E_t -E_{t-1}) [( \varepsilon_{t} - (1+r) \varepsilon_{t-1}) + \beta (\varepsilon_{t+1} - (1+r) \varepsilon_t) ]\\ & = [\varepsilon_{t} - \beta (1+r)\varepsilon_t) ] = 0 \end{align}\)

so there is no inflation and a constant price level. The value of the debt is not constant, however.

\(\begin{align} \frac{B_{t-1}}{P_t} &= E_t (s_t + \beta s_{t+1})\\& = E_t [( \varepsilon_{t} - (1+r) \varepsilon_{t-1}) + \beta ( \varepsilon_{t+1} - (1+r) \varepsilon_t) ] \\ &= -(1+r)\varepsilon_{t-1} . \end{align}\)

The end of period debt is

\(\begin{align} \frac{Q_{t-1}B_{t-1}}{P_{t-1}}&=\beta \frac{B_{t-1}}{P_{t-1}} \\ &= E_{t-1}(\beta s_t + \beta^2 s_{t+1} + ...)\\ & = -\varepsilon_{t-1} \end{align} \)

The debt is exactly equal to the deficit shock at t-1, of course. Debt then forecasts the surplus

\(\begin{align} \varepsilon_{t} - (1+r)\varepsilon_{t-1} &= -(1+r)\varepsilon_{t-1} + \varepsilon_{t} \\ s_{t+1} & = (1+r) \frac{B_{t-1}}{P_{t-1}} + \varepsilon_{t+1} \end{align} \)

This is a regression equation, because the right hand variable is uncorrelated with the error term. If you run a regression of surpluses on debt, it looks like surpluses “respond” to the debt and so fiscal policy is “passive.” But surpluses are completely exogenous in this example, and fiscal policy is totally “active.”

This example is artificial because any deficit gets paid off completely one period later. More realistic examples have the debt paid off slowly over time. That gives a lower positive coefficient on lagged debt. But that specification takes more algebra.

The money-financed government, negative surpluses, and r<g

Imagine a government that finances itself entirely by printing money. There is a money demand, MV=PY, by which people are willing to hold that money.

This situation can still represent 100% fiscal theory of the price level. The price level is still determined by the condition that the real value of money must equal the present value of surpluses, including seignorage revenue. The government provides money “passively,” providing M in response to PY/V. The Fed was charged to “furnish an elastic currency” in the original Federal Reserve act, which means essentially this. The Fed currently allows banks to freely obtain cash in return for interest-paying reserves which is essentially such a policy.

The primary surplus can be perpetually negative, financed by that seigniorage. Perpetually negative surpluses do not invalidate fiscal theory. The rate of return on government debt, which is the negative of the inflation rate, is less than the economy’s growth rate, so “r<g.” The present value relation converges nonetheless. It is a mistake to discount surpluses, ignoring seigniorage, at the average return. It seems that debt (money) does not have to be repaid, since primary surpluses are always negative.

Money is outstanding and surpluses are always negative. It’s tempting to conclude that debt does not have to be repaid, that fiscal expansion is costless. But the opportunity obviously does not scale. More money means more inflation.

Equations:

When we add money to fiscal theory in the simplest way — add MV=PY, all M is the base (no inside money), and M does not pay interest — the basic valuation equation becomes (FTPL 3.4)

\(\frac{B_{t-1}+M_{t-1}}{P_t} = \sum_{j=0}^\infty \beta^j \left( s_{t+j} + \frac{i_{t+j}}{1+i_{t+j}}\frac{M_{t+j}}{P_{t+j}} \right) \;\; (6)\)

The algebra will be easier in continuous time,

\(\frac{M_t+B_t}{P_t} = E_t \int_{\tau=0}^\infty e^{-r\tau} \left( s_{t+\tau} + i_{t+\tau}\frac{M_{t+\tau}}{P_{t+\tau}}\right)d\tau\)

Money is just another form of government debt. But since people are willing to hold money at no interest, the interest savings from issuing money rather than debt shows up as a surplus. “Liquidity effects” in government bonds, or default premiums, show up similarly.

The parable simplifies to a government that issues only money, so B_t=0. The price level is still determined by the condition that the real value of money must equal the present value of surpluses. This is still a 100% fiscal theory economy. M=PY/V then makes sure that MV=PY.

With a steady money growth, steady inflation 𝜋, we will have a steady real money M/P. We also have i=r+𝜋. The valuation equation then becomes

\(\begin{align} \frac{M}{P} &= \int_{\tau=0}^\infty e^{-r \tau} \left( s + i \frac{M}{P} \right) d\tau \\ r\frac{M}{P} & = s + i \frac{M}{P}\\ s &= -\pi \frac{M}{P} \end{align} \)

The surplus can be perpetually slightly negative, financed by the seignorage revenue of money.

Perpetually negative surpluses do not doom FTPL. The right hand side of the present value relation is positive and finite.

The rate of return on government debt is -𝜋, so “r” the return on government debt is less than “g,” zero here. If you try to discount a negative primary surplus at a negative discount rate, the present value formula would indeed blow up. That’s the wrong thing to do for a number of reasons. (See “r<g” in FTPL.) Beware: you can’t take the average return on government debt and apply a frictionless perfect foresight discount formula.